| 2007/04/30 07:55 | 予想レンジ | ストップロスオーダー | ||||
|---|---|---|---|---|---|---|
| 通貨ペア | 前日終値 | 下値 | 上値 | 戦略 | 下値 | 上値 |
| USD/JPY | 119.4700 | 118.9968 | 120.0232 | 買 | 118.5042 | 120.5159 |
| EUR/USD | 1.3655 | 1.3613 | 1.3718 | 買 | 1.3563 | 1.3768 |
| EUR/JPY | 163.1700 | 162.8053 | 163.9316 | 買 | 162.2647 | 164.4722 |
| GBP/USD | 1.9983 | 1.9917 | 2.0057 | 買 | 1.9849 | 2.0125 |
| GBP/JPY | 238.7700 | 238.1020 | 239.9018 | 買 | 237.2382 | 240.7656 |
| AUD/USD | 0.8304 | 0.8255 | 0.8348 | 売 | 0.8211 | 0.8392 |
| AUD/JPY | 99.2000 | 98.7874 | 99.6764 | 買 | 98.3607 | 100.1032 |
| CHF/USD | 0.8297 | 0.8260 | 0.8336 | 買 | 0.8223 | 0.8373 |
| CHF/JPY | 99.1100 | 98.8405 | 99.5369 | 買 | 98.5063 | 99.8712 |
| EGP/USD | 0.1763 | 0.1762 | 0.1765 | 買 | 0.1761 | 0.1766 |
| EGB/JPY | 21.0600 | 20.9853 | 21.1714 | 買 | 20.8959 | 21.2607 |
| JOD/USD | 1.4128 | 1.4123 | 1.4133 | 売 | 1.4118 | 1.4138 |
| JOD/JPY | 168.7900 | 168.1306 | 169.6643 | 買 | 167.3945 | 170.4005 |
| QAR/USD | 0.2747 | 0.2746 | 0.2747 | 売 | 0.2746 | 0.2748 |
| QAR/JPY | 32.8200 | 32.6942 | 32.9873 | 買 | 32.5536 | 33.1280 |
| SAR/USD | 0.2668 | 0.2667 | 0.2669 | 買 | 0.2667 | 0.2669 |
| SAR/JPY | 31.8800 | 31.7647 | 32.0403 | 買 | 31.6324 | 32.1725 |
| TND/USD | 0.7398 | 0.7392 | 0.7404 | 買 | 0.7387 | 0.7410 |
| TND/JPY | 88.3800 | 88.0730 | 88.8084 | 買 | 87.7201 | 89.1614 |
| NZD/USD | 0.7427 | 0.7389 | 0.7467 | 買 | 0.7352 | 0.7505 |
2007年4月30日月曜日
予想レンジ(07/04/30 7:55)
2007年4月27日金曜日
予想レンジ(07/04/27 11:15)
| 2007/04/27 11:14 | 予想レンジ | ストップロスオーダー | ||||
|---|---|---|---|---|---|---|
| 通貨ペア | 前日終値 | 下値 | 上値 | 戦略 | 下値 | 上値 |
| USD/JPY | 119.5300 | 119.0734 | 120.0751 | 買 | 118.5926 | 120.5559 |
| EUR/USD | 1.3593 | 1.3546 | 1.3647 | 買 | 1.3497 | 1.3696 |
| EUR/JPY | 162.5000 | 161.9873 | 163.3203 | 買 | 161.3474 | 163.9602 |
| GBP/USD | 1.9904 | 1.9833 | 1.9976 | 買 | 1.9764 | 2.0045 |
| GBP/JPY | 237.9600 | 237.2608 | 239.0086 | 買 | 236.4218 | 239.8476 |
| AUD/USD | 0.8263 | 0.8219 | 0.8309 | 買 | 0.8176 | 0.8352 |
| AUD/JPY | 98.7600 | 98.3057 | 99.2887 | 買 | 97.8338 | 99.7605 |
| CHF/USD | 0.8273 | 0.8241 | 0.8315 | 買 | 0.8206 | 0.8350 |
| CHF/JPY | 98.8900 | 98.5366 | 99.4247 | 買 | 98.1103 | 99.8510 |
| EGP/USD | 0.1763 | 0.1762 | 0.1764 | 買 | 0.1761 | 0.1765 |
| EGB/JPY | 21.0700 | 20.9945 | 21.1630 | 買 | 20.9136 | 21.2439 |
| JOD/USD | 1.4128 | 1.4121 | 1.4135 | 売 | 1.4115 | 1.4141 |
| JOD/JPY | 168.8800 | 168.2761 | 169.5908 | 買 | 167.6450 | 170.2219 |
| QAR/USD | 0.2747 | 0.2746 | 0.2747 | 売 | 0.2746 | 0.2748 |
| QAR/JPY | 32.8400 | 32.7213 | 32.9784 | 買 | 32.5978 | 33.1018 |
| SAR/USD | 0.2667 | 0.2666 | 0.2668 | 売 | 0.2665 | 0.2668 |
| SAR/JPY | 31.8700 | 31.7569 | 32.0007 | 買 | 31.6399 | 32.1177 |
| TND/USD | 0.7398 | 0.7393 | 0.7407 | 買 | 0.7386 | 0.7413 |
| TND/JPY | 88.4200 | 88.1113 | 88.8254 | 買 | 87.7686 | 89.1681 |
| NZD/USD | 0.7386 | 0.7350 | 0.7429 | 買 | 0.7313 | 0.7466 |
2007年4月26日木曜日
予想レンジ(07/04/26 11:50)
| 2007/04/26 | 前終値 | 下値 | 上値 | 戦略 |
|---|---|---|---|---|
| USD/JPY | 118.5000 | 118.1003 | 118.9127 | 買 |
| EUR/USD | 1.3652 | 1.3613 | 1.3705 | 買 |
| EUR/JPY | 161.7800 | 161.2501 | 162.5238 | 買 |
| GBP/USD | 2.0049 | 1.9998 | 2.0110 | 買 |
| GBP/JPY | 237.5900 | 236.8042 | 238.5762 | 買 |
| AUD/USD | 0.8332 | 0.8292 | 0.8376 | 買 |
| AUD/JPY | 98.7500 | 98.2669 | 99.2811 | 買 |
| CHF/USD | 0.8315 | 0.8286 | 0.8353 | 買 |
| CHF/JPY | 98.5200 | 98.1399 | 99.0075 | 買 |
| EGP/USD | 0.1763 | 0.1762 | 0.1764 | 買 |
| EGB/JPY | 20.8900 | 20.8255 | 20.9595 | 買 |
| JOD/USD | 1.4126 | 1.4119 | 1.4133 | 買 |
| JOD/JPY | 167.4000 | 166.8848 | 167.9133 | 売 |
| QAR/USD | 0.2748 | 0.2748 | 0.2748 | 買 |
| QAR/JPY | 32.5600 | 32.4589 | 32.6606 | 売 |
| SAR/USD | 0.2669 | 0.2668 | 0.2670 | 買 |
| SAR/JPY | 31.6200 | 31.5225 | 31.7188 | 買 |
| TND/USD | 0.7398 | 0.7393 | 0.7405 | 買 |
| TND/JPY | 87.6600 | 87.3795 | 87.9591 | 買 |
| NZD/USD | 0.7457 | 0.7428 | 0.7498 | 買 |
2007年4月25日水曜日
予想レンジ(07/04/25 11:55)
usdjpy 118.1184 118.9834
eurusd 1.3593 1.3689
eurjpy 161.0726 162.4029
gbpusd 1.9974 2.0087
gbpjpy 236.5823 238.4249
audusd 0.8254 0.8335
audjpy 97.8948 98.8593
nzdusd 0.7405 0.7475
eurusd 1.3593 1.3689
eurjpy 161.0726 162.4029
gbpusd 1.9974 2.0087
gbpjpy 236.5823 238.4249
audusd 0.8254 0.8335
audjpy 97.8948 98.8593
nzdusd 0.7405 0.7475
2007年4月24日火曜日
予想レンジ(07/04/24 13:50)
usdjpy 117.8948 118.8849
eurusd 1.3540 1.3633
eurjpy 160.1690 161.4961
gbpusd 1.9952 2.0095
gbpjpy 236.1250 238.0101
2007年4月23日月曜日
2007年4月19日木曜日
相対的購買力平価(USD/JPY)

解析条件
(S_m - S_n)/S_n = (PJ_m - PJ_n)/PJ_n - (PU_m - PU_n)/PU_n
m = n+1
日本の物価指数(PJ) : 企業物価指数 (CGPI Corporate Goods Price Index)
: 日消費者物価指数(CPI Consumer Price Index)
海外の物価指数(PU) : 米生産者物価指数 (PPI Producer Price Index)
: 米消費者物価指数 (CPI Consumer Price Index)
基準年 : 1973 (1ドル = 265円)
年/月 実現 予測(CGPI,PPI) 予測(CPI)
2000/01 106.90 138.36 179.11
2001/01 116.38 123.27 171.74
2002/01 132.94 130.02 167.33
2003/01 119.21 121.79 162.34
2004/01 105.88 116.30 158.64
2005/01 103.58 110.08 154.35
2006/01 117.18 103.27 147.99
2007/01 121.34 105.52 144.90
2007年4月18日水曜日
回帰分析による相対的購買力平価 2(USD/JPY)

解析条件
相対的購買力平価=基準時点の為替相場×日本の物価指数÷海外の物価指数
日本の物価指数:日消費者物価指数 (CPI Consumer Price Index)
海外の物価指数: 米消費者物価指数 (CPI Consumer Price Index)
基準年 : 1973(CPI(日) = CPI(米) = 100)
年/月 実現 予測
2000/01 106.90 120.35
2001/01 116.38 113.51
2002/01 132.94 109.36
2003/01 119.21 104.78
2004/01 105.88 101.41
2005/01 103.58 97.57
2006/01 117.18 92.02
2007/01 121.34 89.31
2007年4月17日火曜日
回帰分析による相対的購買力平価(USD/JPY)

解析条件
相対的購買力平価=基準時点の為替相場×日本の物価指数÷海外の物価指数
日本の物価指数 :企業物価指数(CGPI Corporate Goods Price Index)
海外の物価指数 :米生産者物価指数(PPI Producer Price Index)
基準年 :1973(CGPI = PPI = 100)
年/月 実現 予測
00/01 106.90 122.60
01/01 116.38 107.58
02/01 132.94 115.61
03/01 119.21 107.05
04/01 105.88 101.35
05/01 103.58 95.08
06/01 117.18 88.42
07/01 121.34 90.83
USD/JPYは円安過ぎ?
2007年4月14日土曜日
サイコロによるベルヌイ試行
2007年4月13日金曜日
モンテカルロ法によるPIの推定(ビフォンの問題)
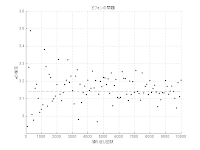
%ビフォンの問題
No = 100;
D = 0.2;
L = 0.1;
line = L/2:D:1-L/2
for j=1:No
N = j*100;
y = rand(N,1);
theta = rand(N,1)*pi/2;
y1 = y + L/2*cos(theta);
y2 = y - L/2*cos(theta);
s = 0;
for i=1:length(line)
s = s + sum( (line(i) >= y1) == (line(i) <= y2) );
end
%
% p = 2*L/(pi*D)
%
p = s/N
PI(j) = 2*L/(D*p);
NS(j) = N;
end
hold on;
plot(NS,PI,'.k');
plot(NS,ones(No,1)*pi,'--r');
title('ビフォンの問題');
xlabel('繰り返し回数');
ylabel('\piの推定');
grid on;
hold off;
print('-dpng','-r80','pi_buffo.png');
2007年4月12日木曜日
モンテカルロ法によるPIの推定

%モンテカルロ法によるPIの推定
No = 100;
for i=1:No
N = 100*i;
x = rand(N,1); %一様分布の擬似乱数
y = rand(N,1); %一様分布の擬似乱数
r = x.^2+y.^2;
NS(i) = N;
PI(i) = 4*sum(r<1)/N;
end
r = 1;
c = 2;
subplot(r,c,1);
hold on;
plot(NS,PI,'.k');
plot(NS,ones(No,1)*pi,'--r');
xlabel('繰り返し回数');
ylabel('\piの推定');
grid on;
hold off;
subplot(r,c,2);
hold on;
t = 0:0.01:pi/2;
rx = cos(t);
ry = sin(t);
plot(rand(No*100,1),rand(No*100,1),'.k');
plot(rx,ry,'r');
grid on;
hold off;
print('-dpng','-r80','pi_mento.png');
2007年4月10日火曜日
対応なしのt検定:2 標本の平均値の差の検定
%MATLABの場合
echo on
N1 = 20;
N2 = 30;
x = rand(N1,1); % 標本1の一様分布の擬似乱数
x_mea = mean(x); % 標本1の平均値
disp(x_mea);
0.5539
x_std = std(x); % 標本1の不偏標準偏差
disp(x_std);
0.3199
y = rand(N2,1); % 標本2の一様分布の擬似乱数
y_mea = mean(y); % 標本2の平均値
disp(y_mea);
0.5384
y_std = std(y); % 標本2の不偏標準偏差
disp(y_std);
0.2955
%帰無仮説: x_mea(標本1の平均値)は,y_mea(標本1の平均値)である
%対立仮説: x_mea(標本1の平均値)は,y_mea(標本1の平均値)ではない
%両側5%有意水準でttest2を実行する
%2つの独立な標本が平均の等しい分布
[h,p,ci,stats] = ttest2(x,y); %共同(pooled)または共同ではない(unpooled)分散をもつ2標本T-検定
str = sprintf('h = %1.2f, p = %f, ci = [%f,%f]',h,p,ci(1),ci(2));
%h = 0 -> 帰無仮説は、棄却しない。つまり、x_mea(標本1の平均値)は,x_mea(標本2の平均値)である
disp(str);
h = 0.00, p = 0.861089, ci = [-0.161731,0.192748]
disp(stats);
tstat: 0.1759
df: 48
sd: 0.3054
disp(stats.sd);
0.3054
%2つの標本が、未知、または等しくない分散
[h,p,ci,stats] = ttest2(x,y,[],[],'unequal'); %共同(pooled)または共同ではない(unpooled)分散をもつ2標本T-検定
str = sprintf('h = %1.2f, p = %f, ci = [%f,%f]',h,p,ci(1),ci(2));
%h = 0 -> 帰無仮説は、棄却しない。つまり、x_mea(標本1の平均値)は,x_mea(標本2の平均値)である
disp(str);
h = 0.00, p = 0.863469, ci = [-0.165760,0.196777]
disp(stats);
tstat: 0.1731
df: 38.5863
sd: [2x1 double]
disp(stats.sd);
0.3199
0.2955
echo on
N1 = 20;
N2 = 30;
x = rand(N1,1); % 標本1の一様分布の擬似乱数
x_mea = mean(x); % 標本1の平均値
disp(x_mea);
0.5539
x_std = std(x); % 標本1の不偏標準偏差
disp(x_std);
0.3199
y = rand(N2,1); % 標本2の一様分布の擬似乱数
y_mea = mean(y); % 標本2の平均値
disp(y_mea);
0.5384
y_std = std(y); % 標本2の不偏標準偏差
disp(y_std);
0.2955
%帰無仮説: x_mea(標本1の平均値)は,y_mea(標本1の平均値)である
%対立仮説: x_mea(標本1の平均値)は,y_mea(標本1の平均値)ではない
%両側5%有意水準でttest2を実行する
%2つの独立な標本が平均の等しい分布
[h,p,ci,stats] = ttest2(x,y); %共同(pooled)または共同ではない(unpooled)分散をもつ2標本T-検定
str = sprintf('h = %1.2f, p = %f, ci = [%f,%f]',h,p,ci(1),ci(2));
%h = 0 -> 帰無仮説は、棄却しない。つまり、x_mea(標本1の平均値)は,x_mea(標本2の平均値)である
disp(str);
h = 0.00, p = 0.861089, ci = [-0.161731,0.192748]
disp(stats);
tstat: 0.1759
df: 48
sd: 0.3054
disp(stats.sd);
0.3054
%2つの標本が、未知、または等しくない分散
[h,p,ci,stats] = ttest2(x,y,[],[],'unequal'); %共同(pooled)または共同ではない(unpooled)分散をもつ2標本T-検定
str = sprintf('h = %1.2f, p = %f, ci = [%f,%f]',h,p,ci(1),ci(2));
%h = 0 -> 帰無仮説は、棄却しない。つまり、x_mea(標本1の平均値)は,x_mea(標本2の平均値)である
disp(str);
h = 0.00, p = 0.863469, ci = [-0.165760,0.196777]
disp(stats);
tstat: 0.1731
df: 38.5863
sd: [2x1 double]
disp(stats.sd);
0.3199
0.2955
対応ありのt検定:2 標本の平均値の差の検定
%MATLABの場合
echo on
N = 20;
x = rand(N,1); % 標本1の一様分布の擬似乱数
x_mea = mean(x); % 標本1の平均値
disp(x_mea);
0.5653
x_std = std(x); % 標本1の不偏標準偏差
disp(x_std);
0.2773
y = rand(N,1); % 標本2の一様分布の擬似乱数
y_mea = mean(y); % 標本2の平均値
disp(y_mea);
0.4351
y_std = std(y); % 標本2の不偏標準偏差
disp(y_std);
0.1968
d = x - y;
d_mea = mean(d);
disp(d_mea);
0.1301
%帰無仮説: x_mea(標本1の平均値)は,y_mea(標本1の平均値)である
%対立仮説: x_mea(標本1の平均値)は,y_mea(標本1の平均値)ではない
%両側5%有意水準でttestを実行する
[h,p,ci,stats] = ttest(d,0); %1標本と対標本T-検定
str = sprintf('h = %1.2f, p = %f, ci = [%f,%f]',h,p,ci(1),ci(2));
%h = 0 -> 帰無仮説は、棄却しない。つまり、x_mea(標本1の平均値)は,x_mea(標本2の平均値)である
disp(str);
h = 0.00, p = 0.120141, ci = [-0.037243,0.297517]
disp(stats);
tstat: 1.6273
df: 19
sd: 0.3576
echo on
N = 20;
x = rand(N,1); % 標本1の一様分布の擬似乱数
x_mea = mean(x); % 標本1の平均値
disp(x_mea);
0.5653
x_std = std(x); % 標本1の不偏標準偏差
disp(x_std);
0.2773
y = rand(N,1); % 標本2の一様分布の擬似乱数
y_mea = mean(y); % 標本2の平均値
disp(y_mea);
0.4351
y_std = std(y); % 標本2の不偏標準偏差
disp(y_std);
0.1968
d = x - y;
d_mea = mean(d);
disp(d_mea);
0.1301
%帰無仮説: x_mea(標本1の平均値)は,y_mea(標本1の平均値)である
%対立仮説: x_mea(標本1の平均値)は,y_mea(標本1の平均値)ではない
%両側5%有意水準でttestを実行する
[h,p,ci,stats] = ttest(d,0); %1標本と対標本T-検定
str = sprintf('h = %1.2f, p = %f, ci = [%f,%f]',h,p,ci(1),ci(2));
%h = 0 -> 帰無仮説は、棄却しない。つまり、x_mea(標本1の平均値)は,x_mea(標本2の平均値)である
disp(str);
h = 0.00, p = 0.120141, ci = [-0.037243,0.297517]
disp(stats);
tstat: 1.6273
df: 19
sd: 0.3576
母分散の検定:母平均が既知・未知
%MATLABの場合
echo on
N = 10000;
data = rand(N,1); % 母集団の一様分布の擬似乱数
d_mea = mean(data); % 母集団の平均値
disp(d_mea);
0.4990
d_std = std(data,1);
disp(d_std);
0.2903
SN = 20;
sdata = rand(SN,1); % 標本の一様分布の擬似乱数
s_mea = mean(sdata); % 標本の平均値
disp(s_mea);
0.5670
s_std = std(sdata); % 標本の不偏標準偏差
disp(s_std);
0.2542
%帰無仮説: s_std(標本の不偏標準偏差)は,d_std(母集団の標準偏差)である
%対立仮説: s_std(標本の不偏標準偏差)は,d_std(母集団の標準偏差)ではない
%母平均が既知
%http://www.cybernet.co.jp/matlab/library/library/file/T/chi2test_var.m
[h,p,ci,stats]=chi2test_var(sdata,d_std^2,d_mea);
str = sprintf('h = %1.2f, p = %f, ci = [%f,%f]',h,p,ci(1),ci(2));
%h = 0 -> 帰無仮説は、棄却しない。つまり、s_std(標本の不偏標準偏差)は,d_std(母集団の標準偏差)である
disp(str);
h = 0.00, p = 0.526566, ci = [0.038656,0.137721]
disp(stats);
chi2stat: 15.6726
df: 20
%母平均が未知
[h,p,ci,stats]=chi2test_var(sdata,d_std^2,[]);
str = sprintf('h = %1.2f, p = %f, ci = [%f,%f]',h,p,ci(1),ci(2));
%h = 0 -> 帰無仮説は、棄却しない。つまり、s_std(標本の不偏標準偏差)は,d_std(母集団の標準偏差)である
disp(str);
h = 0.00, p = 0.501376, ci = [0.037385,0.137899]
disp(stats);
chi2stat: 14.5732
df: 19
echo on
N = 10000;
data = rand(N,1); % 母集団の一様分布の擬似乱数
d_mea = mean(data); % 母集団の平均値
disp(d_mea);
0.4990
d_std = std(data,1);
disp(d_std);
0.2903
SN = 20;
sdata = rand(SN,1); % 標本の一様分布の擬似乱数
s_mea = mean(sdata); % 標本の平均値
disp(s_mea);
0.5670
s_std = std(sdata); % 標本の不偏標準偏差
disp(s_std);
0.2542
%帰無仮説: s_std(標本の不偏標準偏差)は,d_std(母集団の標準偏差)である
%対立仮説: s_std(標本の不偏標準偏差)は,d_std(母集団の標準偏差)ではない
%母平均が既知
%http://www.cybernet.co.jp/matlab/library/library/file/T/chi2test_var.m
[h,p,ci,stats]=chi2test_var(sdata,d_std^2,d_mea);
str = sprintf('h = %1.2f, p = %f, ci = [%f,%f]',h,p,ci(1),ci(2));
%h = 0 -> 帰無仮説は、棄却しない。つまり、s_std(標本の不偏標準偏差)は,d_std(母集団の標準偏差)である
disp(str);
h = 0.00, p = 0.526566, ci = [0.038656,0.137721]
disp(stats);
chi2stat: 15.6726
df: 20
%母平均が未知
[h,p,ci,stats]=chi2test_var(sdata,d_std^2,[]);
str = sprintf('h = %1.2f, p = %f, ci = [%f,%f]',h,p,ci(1),ci(2));
%h = 0 -> 帰無仮説は、棄却しない。つまり、s_std(標本の不偏標準偏差)は,d_std(母集団の標準偏差)である
disp(str);
h = 0.00, p = 0.501376, ci = [0.037385,0.137899]
disp(stats);
chi2stat: 14.5732
df: 19
2007年4月9日月曜日
母平均の検定( t検定 ):母集団の平均値が既知,分散が未知
%MATLABの場合
echo on
N = 10000;
data = rand(N,1); % 母集団の一様分布の擬似乱数
d_mea = mean(data); % 母集団の平均値
disp(d_mea);
0.4975
SN = 20;
sdata = rand(SN,1); % 標本の一様分布の擬似乱数
s_mea = mean(sdata); % 標本の平均値
%帰無仮説: s_mea(標本の平均値)は,d_mea(母集団の平均値)である
%対立仮説: s_mea(標本の平均値)は,d_mea(母集団の平均値)ではない
disp(s_mea);
0.4303
s_std = std(sdata); % 標本の不偏標準偏差
disp(s_std);
0.3290
%両側5%有意水準でztestを実行する
[h,p,ci,stats] = ttest(sdata,d_mea); %1標本と対標本T-検定
str = sprintf('h = %1.2f, p = %f, ci = [%f,%f]',h,p,ci(1),ci(2));
%h = 0 -> 帰無仮説は、棄却しない。つまり、s_mea(標本の平均値)は,d_mea(母集団の平均値)である
disp(str);
h = 0.00, p = 0.372482, ci = [0.276294,0.584258]
disp(stats);
tstat: -0.9134
df: 19
sd: 0.3290
echo on
N = 10000;
data = rand(N,1); % 母集団の一様分布の擬似乱数
d_mea = mean(data); % 母集団の平均値
disp(d_mea);
0.4975
SN = 20;
sdata = rand(SN,1); % 標本の一様分布の擬似乱数
s_mea = mean(sdata); % 標本の平均値
%帰無仮説: s_mea(標本の平均値)は,d_mea(母集団の平均値)である
%対立仮説: s_mea(標本の平均値)は,d_mea(母集団の平均値)ではない
disp(s_mea);
0.4303
s_std = std(sdata); % 標本の不偏標準偏差
disp(s_std);
0.3290
%両側5%有意水準でztestを実行する
[h,p,ci,stats] = ttest(sdata,d_mea); %1標本と対標本T-検定
str = sprintf('h = %1.2f, p = %f, ci = [%f,%f]',h,p,ci(1),ci(2));
%h = 0 -> 帰無仮説は、棄却しない。つまり、s_mea(標本の平均値)は,d_mea(母集団の平均値)である
disp(str);
h = 0.00, p = 0.372482, ci = [0.276294,0.584258]
disp(stats);
tstat: -0.9134
df: 19
sd: 0.3290
母平均の検定( Z検定 ):母集団の平均値と分散が既知
%MATLABの場合
echo on
N = 10000;
data = rand(N,1); % 母集団の一様分布の擬似乱数
d_mea = mean(data); % 母集団の平均値
disp(d_mea);
0.4950
d_std = std(data,1); % 母集団の偏標準偏差
disp(d_std);
0.2877
SN = 20;
sdata = rand(SN,1); % 標本の一様分布の擬似乱数
s_mea = mean(sdata); % 標本の平均値
%帰無仮説: s_mea(標本の平均値)は,d_mea(母集団の平均値)である
%対立仮説: s_mea(標本の平均値)は,d_mea(母集団の平均値)ではない
disp(s_mea);
0.4455
s_std = std(sdata); % 標本の不偏標準偏差
disp(s_std);
0.2397
%両側5%有意水準でztestを実行する
[h,p,ci,zval] = ztest(sdata,d_mea,d_std); %1標本Z-検定
str = sprintf('h = %1.2f, p = %f, ci = [%f,%f], zval = %f',h,p,ci(1),ci(2),zval);
%h = 0 -> 帰無仮説は、棄却しない。つまり、s_mea(標本の平均値)は,d_mea(母集団の平均値)である
disp(str);
h = 0.00, p = 0.442067, ci = [0.319444,0.571654], zval = -0.768707
echo on
N = 10000;
data = rand(N,1); % 母集団の一様分布の擬似乱数
d_mea = mean(data); % 母集団の平均値
disp(d_mea);
0.4950
d_std = std(data,1); % 母集団の偏標準偏差
disp(d_std);
0.2877
SN = 20;
sdata = rand(SN,1); % 標本の一様分布の擬似乱数
s_mea = mean(sdata); % 標本の平均値
%帰無仮説: s_mea(標本の平均値)は,d_mea(母集団の平均値)である
%対立仮説: s_mea(標本の平均値)は,d_mea(母集団の平均値)ではない
disp(s_mea);
0.4455
s_std = std(sdata); % 標本の不偏標準偏差
disp(s_std);
0.2397
%両側5%有意水準でztestを実行する
[h,p,ci,zval] = ztest(sdata,d_mea,d_std); %1標本Z-検定
str = sprintf('h = %1.2f, p = %f, ci = [%f,%f], zval = %f',h,p,ci(1),ci(2),zval);
%h = 0 -> 帰無仮説は、棄却しない。つまり、s_mea(標本の平均値)は,d_mea(母集団の平均値)である
disp(str);
h = 0.00, p = 0.442067, ci = [0.319444,0.571654], zval = -0.768707
データの不偏分散,不偏標準偏差
> #統計R解析の場合
> data <- runif(10000) #一様乱数を発生させる関数( 0.0 - 1.0 ) > d_var <- var(data) # 不偏分散 > d_var
[1] 0.08373053
> d_sd <- sd(data) # 不偏標準偏差 > d_sd
[1] 0.2893623
>
%MATLABの場合
echo on
N = 10000;
data = rand(N,1); % 一様分布の擬似乱数
d_var = var(data); % 不偏分散
disp(d_var);
0.0842
d_std = std(data); % 不偏標準偏差
disp(d_std);
0.2901
> data <- runif(10000) #一様乱数を発生させる関数( 0.0 - 1.0 ) > d_var <- var(data) # 不偏分散 > d_var
[1] 0.08373053
> d_sd <- sd(data) # 不偏標準偏差 > d_sd
[1] 0.2893623
>
%MATLABの場合
echo on
N = 10000;
data = rand(N,1); % 一様分布の擬似乱数
d_var = var(data); % 不偏分散
disp(d_var);
0.0842
d_std = std(data); % 不偏標準偏差
disp(d_std);
0.2901
2007年4月8日日曜日
データの代表値
> #Rの場合
> data <- runif(10000) #一様乱数を発生させる関数( 0.0 - 1.0 ) > le <- length(data) # > le[1] 10000> mea <- mean(data) #平均値( mean ) > mea[1] 0.4992161
> med <- median(data) #中央値( median ) > med[1] 0.4970672
> ran <- range(data) #範囲( range ) > ran[1] 0.0001207402 0.9997703242
%MATLABの場合
echo on
data = rand(1000,1); %一様分布の擬似乱数
len = length(data); %ベクトルの長さ
disp(len);
1000
mea = mean(data); %配列の平均値
disp(mea);
0.4925
med = median(data); %配列の中央値
disp(med);
0.4915
> data <- runif(10000) #一様乱数を発生させる関数( 0.0 - 1.0 ) > le <- length(data) # > le[1] 10000> mea <- mean(data) #平均値( mean ) > mea[1] 0.4992161
> med <- median(data) #中央値( median ) > med[1] 0.4970672
> ran <- range(data) #範囲( range ) > ran[1] 0.0001207402 0.9997703242
%MATLABの場合
echo on
data = rand(1000,1); %一様分布の擬似乱数
len = length(data); %ベクトルの長さ
disp(len);
1000
mea = mean(data); %配列の平均値
disp(mea);
0.4925
med = median(data); %配列の中央値
disp(med);
0.4915
登録:
投稿 (Atom)




